Der A-Star Algorithmus mit iterativer Vertiefung (IDA & ast;) ist ein Algorithmus, der verwendet wird, um das Problem des kürzesten Pfades in einem Baum zu lösen, kann jedoch modifiziert werden, um Graphen (d. H. Zyklen) zu handhaben. Es baut auf der ID-DFS (Iterative Deepening Depth-First Search) auf, indem eine Heuristik hinzugefügt wird, um nur relevante Knoten zu untersuchen.

Beschreibung des Algorithmus

Während Iterative Deepening DFS eine einfache Tiefe verwendet, um zu entscheiden, wann die aktuelle Iteration abgebrochen und mit einer höheren Tiefe fortgesetzt werden soll, Iterative Vertiefung Ein Stern verwendet eine Heuristik, um zu bestimmen, welche Knoten erforscht und in welcher Tiefe gestoppt werden soll. Dies ähnelt der Art und Weise, wie Dijkstra den Knoten immer mit dem derzeit kürzesten Unterschied untersucht und A Star eine Heuristik hinzufügt, um nur Knoten zu untersuchen, die tatsächlich näher am Ziel liegen.

Im Einzelnen führt dies zu den folgenden Schritten:

1. Für jedes Kind des aktuellen Knotens
2. Wenn es sich um den Zielknoten handelt, kehren Sie zurück
3. Wenn der Abstand plus die Heuristik den aktuellen Schwellenwert überschreitet, geben Sie diesen Schwellenwert zurück
4. Setzen Sie den aktuellen Knoten auf diesen Knoten und kehren Sie zu 1 zurück.
5. Nachdem Sie alle Kinder durchlaufen haben, gehen Sie zum nächsten Kind des Elternteils (dem nächsten Geschwister).
6. Nachdem Sie alle untergeordneten Elemente des Startknotens durchlaufen haben, erhöhen Sie den Schwellenwert auf den kleinsten der überschrittenen Schwellenwerte.
7. Wenn wir alle Blattknoten (unten) erreicht haben, existiert der Zielknoten nicht.

Beispiel des Algorithmus

Betrachten Sie das folgende Diagramm:

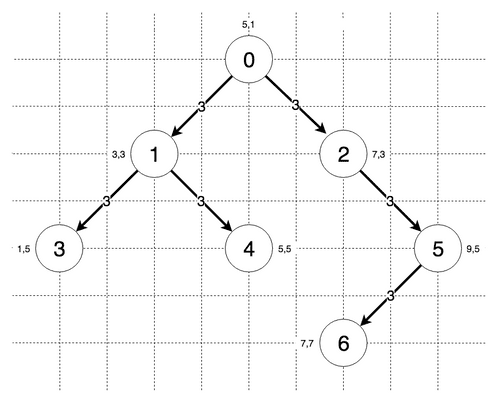
Die Schritte, die der Algorithmus in diesem Diagramm ausführt, wenn Knoten 0 als Startpunkt und Knoten 6 als Ziel in der angegebenen Reihenfolge angegeben werden, sind:

1. Iteration mit Schwelle: 6.32
2. Besuche Knoten 0
3. Besuche Knoten 1
4. Schwelle mit Heuristik überschritten: 8.66
5. Besuche Knoten 2
6. Schwelle mit Heuristik überschritten: 7.00
7. Iteration mit Schwelle: 7.00
8. Besuche Knoten 0
9. Besuche Knoten 1
10. Schwelle mit Heuristik überschritten: 8.66
11. Besuche Knoten 2
12. Besuche Knoten 5
13. Schwelle mit Heuristik überschritten: 8.83
14. Iteration mit Schwelle: 8.66
15. Besuche Knoten 0
16. Besuche Knoten 1
17. Besuche Knoten 3
18. Schwelle mit Heuristik überschritten: 12.32
19. Besuche Knoten 4
20. Schwelle mit Heuristik überschritten: 8.83
21. Besuche Knoten 2
22. Besuche Knoten 5
23. Schwelle mit Heuristik überschritten: 8.83
24. Iteration mit Schwelle: 8,83
25. Besuche Knoten 0
26. Besuche Knoten 1
27. Besuche Knoten 3
28. Schwelle mit Heuristik überschritten: 12.32
29. Besuche Knoten 4
30. Besuche Knoten 2
31. Besuche Knoten 5
32. Besuche Knoten 6
33. Den Knoten gefunden, den wir suchen!

Endgültig niedrigster Abstand von Knoten 0 zu Knoten 6: 9

Beachten Sie, dass der Algorithmus in der Iteration, in der er den Zielknoten gefunden hat, nicht weiter von Knoten 3 aus nach unten gesucht hat. Wenn Knoten 3 Kinder gehabt hätte, während Iterative Deepening DFS sie möglicherweise (und unnötig!) Erkundet hätte, hätte Iterative Deepening A Star dies nicht getan.

Laufzeit des Algorithmus

Die Laufzeitkomplexität von Iterative Deepening A Star entspricht im Prinzip der von Iterative Deepening DFS. In der Praxis können jedoch viele der Pfade eliminiert werden, bevor wir untersucht werden, wenn wir eine gute Heuristik wählen, was zu einer signifikanten Zeitverbesserung führt. Weitere Informationen darüber, wie die Heuristik die Komplexität beeinflusst, finden Sie im Wikipedia-Artikel.

Speicherkomplexität des Algorithmus

Die räumliche Komplexität von Iterative Deepening A Star ist die Speichermenge, die für den Baum oder das Diagramm benötigt wird. O(| N|), |N| = Anzahl der Knoten im Baum oder Diagramm, die für Bäume durch b^d ersetzt werden können, wobei b der Verzweigungsfaktor und d ist die Tiefe. Unabhängig davon, welchen Platz die Heuristik benötigt.