The A star (A*) algorithm is an algorithm used to solve the shortest path problem in a graph. This means that given a number of nodes and the edges between them as well as the “length” of the edges (referred to as “weight”) and a heuristic (more on that later), the A* algorithm finds the shortest path from the specified start node to all other nodes. Nodes are sometimes referred to as vertices (plural of vertex) - here, we’ll call them nodes.

Description of the Algorithm

The basic principle behind the A star (A*) algorithm is to iteratively look at the node with the currently smallest priority (which is the shortest distance from the start plus the heuristic to the goal) and update all not yet visited neighbors if the path to it via the current node is shorter. This is very similar to the Dijkstra algorithm, with the difference being that the lowest priority node is visited next, rather than the shortest distance node. In essence, Dijkstra uses the distance as the priority, whereas A* uses the distance plus the heuristic.

Why does adding the heuristic make sense? Without it, the algorithm has no idea if its going in the right direction. When manually searching for the shortest path in this example, you probably prioritised paths going to the right over paths going up or down. This is because the goal node is to the right of the start node, so going right is at least generally the correct direction. The heuristic gives the algorithm this spatial information.

So if a node has the currently shortest distance but is generally going in the wrong direction, whereas Dijkstra would have visited that node next, A Star will not. For this to work, the heuristic needs to be admissible, meaning it has to never overestimate the actual cost (i.e. distance) - which is the case for straight line distance in street networks, for example. Intuitively, that way the algorithm never overlooks a shorter path because the priority will always be lower than the real distance (if the current shortest path is A, then if there is any way path B could be shorter it will be explored). One simple heuristic that fulfils this property is straight line distance (e.g. in a street network)

In more detail, this leads to the following Steps:

1. Initialize the distance to the starting node as 0 and the distances to all other nodes as infinite
2. Initialize the priority to the starting node as the straight-line distance to the goal and the priorities of all other nodes as infinite
3. Set all nodes to “unvisited”

4. While we haven’t visited all nodes and haven’t found the goal node:

   1. Find the node with currently lowest priority (for the first pass, this will be the source node itself)
   2. If it’s the goal node, return its distance
   3. For all nodes next to it that we haven’t visited yet, check if the currently smallest distance to that neighbor is bigger than if we were to go via the current node
   4. If it is, update the smallest distance of that neighbor to be the distance from the source to the current node plus the distance from the current node to that neighbor, and update its priority to be the distance plus its straight-line distance to the goal node

Example of the Algorithm

Consider the following graph:

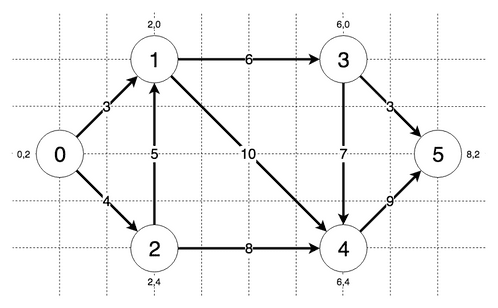
The steps the algorithm performs on this graph if given node 0 as a starting point and node 5 as the goal, in order, are:

1. Visiting node 0 with currently lowest priority of 8.0
2. Updating distance of node 1 to 3 and priority to 9.32455532033676
3. Updating distance of node 2 to 4 and priority to 10.32455532033676
4. Visiting node 1 with currently lowest priority of 9.32455532033676
5. Updating distance of node 3 to 9 and priority to 11.82842712474619
6. Updating distance of node 4 to 13 and priority to 15.82842712474619
7. Visiting node 2 with currently lowest priority of 10.32455532033676
8. Visiting node 3 with currently lowest priority of 11.82842712474619
9. Updating distance of node 5 to 12 and priority to 12.0
10. Goal node found!

Final lowest distance from node 0 to node 5: 12

Runtime of the Algorithm

The runtime complexity of A Star depends on how it is implemented. If a min-heap is used to determine the next node to visit, and adjacency is implemented using adjacency lists, the runtime is O(|E| + |V|log|V|) (|V| = number of Nodes, |E| = number of Edges). If a we simply search all distances to find the node with the lowest distance in each step, and use a matrix to look up whether two nodes are adjacent, the runtime complexity increases to O(|V|^2).

Note that this is the same as Dijkstra - in practice, though, if we choose a good heuristic, many of the paths can be eliminated before they are explored making for a significant time improvement.

More information on how the heuristic influences the complexity can be found on the Wikipedia Article.

Space of the Algorithm

The space complexity of A Star depends on how it is implemented as well and is equal to the runtime complexity, plus whatever space the heuristic requires.

Java™ is a compiled language used for many purposes, ranging from embedded systems, UI-applications to web servers.

Getting to “Hello World” in Java

The most important things first - here’s how you can run your first line of code in Java.

1. Download and install the latest version of Java from java.com. You can also download an earlier version if your use case requires it.

2. Open a terminal, make sure the javac and javac commands are working, and that the command your’re going to be using is referring to the version you just installed by running java -version. If you’re getting a “command not found” error (or similar), try restarting your command line, and, if that doesn’t help, your computer. If the issue persists, here are some helpful StackOverflow questions for each platform:

   • Windows
   • Mac
   • Linux

3. As soon as that’s working, copy the following snippet into a file named HelloWorld.java:

   class HelloWorld {
   public static void main(String[] args) {
       // Paste any following code snippets here.
       System.out.println("Hello World");
   }
   }

4. Change directory by typing cd path/to/HelloWorld, then run javac HelloWorld.java to compile the file (which creates the bytecode), then run java HelloWorld (without the .java ending). This should print “Hello World” to your Terminal.

That’s it! Notice that the entry barrier is a little higher with Java than it is with e.g. Python - but Java is much faster and, in my experience, tends to have fewer bugs in large projects due to strong typing and other factors.

Fundamentals in Java

To understand algorithms and technologies implemented in Java, one first needs to understand what basic programming concepts look like in this particular language. Each of the following snippets should be surrounded by the boilerplate code of the hello world example and should be compiled and run using the commands mentioned above.

Variables and Arithmetic

Variables in Java are statically typed, meaning the content of a variable needs to be specified when writing the code. The datatype for whole numbers, for example is int. Numbers with decimal places are typed float or double depending on the required precision. The type for text ist String.

int number = 5;
double decimalNumber = 3.25;
double result = number * decimalNumber;
String callout = "The number is ";
// In this instance, the values are concatenated rather than added because one of them is a String.
System.out.println(callout + result);

Arrays

Arrays in Java are real arrays (as opposed to e.g. Python where they’re implemented as lists). The implications of that are that the size needs to be set when they are created and cannot be changed, but also that they are more efficient in Java than they are in Python.

int[] integers = new int[5];
integers[3] = 12; // Assigning values to positions in the array
// integers[4] is 0, integers[6] would give IndexOutOfBoundsException
String[] strings = {"Hello", "World"}; // Array initialization with initial values
System.out.println(strings[0] + integers[3]); // Prints "Hello12"

Conditions

Just like most programming languages, Java can do if-else statements. Additionally, Java can also do switch-case statements.

int value = 5;
if(value == 5){
    System.out.println("Value is 5");
} else if(value < 5){
    System.out.println("Value is less than 5");
} else {
    System.out.println("Value is something else");
}

switch (value){
    case 1:
        System.out.println("Value is 1");
        break; // Don't go further down the cases
    case 2:
        System.out.println("Value is 2");
        break; // Don't go further down the cases
    case 3:
        System.out.println("Value is 3");
        break; // Don't go further down the cases
    case 4:
        System.out.println("Value is 4");
        break; // Don't go further down the cases
    case 5:
        System.out.println("Value is 5");
        break; // Don't go further down the cases
    default:
        System.out.println("Value is something else");
}

The above Java code will print “Value is 5” twice.

Loops

Java supports for, while as well as do while loops. break and continue statements are also supported. The below example illustrates the differences:

int value = 2;
for (int i = 0; i < value; i++) {
    System.out.println(i);
}
while (value > 0) {
    System.out.println(value);
    value--;
}
do {
    System.out.println(value);
    value--;
} while (value > 0);

This will print the following to the terminal:

0
1
2
1
0

Note the last 0: it is printed because in the do-while-loop, compared to the while-loop. the code block is executed at least once before the condition is checked.

Functions

Functions in Java can be part of a class, or of an object of a class. For more information on object oriented programming I recommend the w3schools course. Here is a minimal example of a function as part of a class (also called a static function):

class HelloWorld {
    public static void main(String[] args) {
        System.out.println(addNumbers(3, 4));
    }

    public static int addNumbers(int numberOne, int numberTwo) {
        return numberOne + numberTwo;
    }
}

And here’s an example of calling a function of an object of a class:

class HelloWorld {
    public static void main(String[] args) {
        System.out.println(new HelloWorld().addNumbers(3, 4));
    }

    public int addNumbers(int numberOne, int numberTwo) {
        return numberOne + numberTwo;
    }
}

Note how the first example uses the static keyword, and the second example needs to instantiate on object of the class before in can call the function of that object. These are some of the differences in class methods and object functions.

Syntax

Java requires the use of curly brackets ({}) to surround code blocks in conditions, loops, functions etc.; It also requires semicolons at then end of statements. While this can lead to some annoying syntax errors, it also means the use of whitespace for preferred formatting (e.g. indentation of code pieces) does not affect the code.

Advanced Knowledge of Java

Java was first released in 1995 and is multi-paradigm, meaning while it is primarily object-oriented, it also has functional and reflective elements. It’s statically typed, but offers some amount of dynamic typing in recent versions. For more information, Java has a great Wikipedia) article.