The Point in Polygon (PIP) problem is the problem of determining whether a point is any arbitrary polygon. This might sound trivial for a simple polygon like a square or a triangle, but gets more complex with more complex polygons like the one in the example below. In this post, the even-odd algorithm, also called crossing number algorithm or Jordan’s algorithm (since it can be proven using the Jordan curve theorem), will be introduced.

Description of the Algorithm

The basic principle behind the Even-odd aka. Jordan aka. Cross Number Algorithm is to count the number of times a line from the point in question (in any, arbitrary direction) crosses any edge of the polygon. This line will always be outside of the polygon at it’s “end” in infinity, so if it is inside the polygon at the start (the point in question), it will have to leave the polygon at some point, crossing some edge. It can re-enter the polygon (see the example below), but it always has to leave again, making the total number of crossings uneven if the point is in the polygon. The opposite is also true; if the number of crossings is even, the point is always outside of the polygon. This is the above mentioned Jordan’s curve theorem.

The algorithm checks every edge of the polygon in a loop to determine if the line from the point to infinity crosses it. In the example below, this line is drawn from the point to infinity to the right, but it can be any direction.

The steps are:

1. For each edge in the polygon:
2. If the edge crosses the imaginary line from the point to infinity, increase a counter.
3. At then end, if the counter is uneven, return true. Else, return false.

A simple boolean variable that is inverted every time a crossing is found is also possible.

Example of the Algorithm

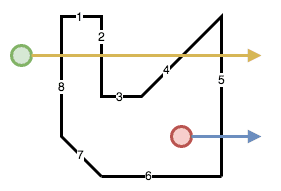
Consider the following polygon with 8 edges and two points for which we want to determine whether they are in the polygon:

The steps the algorithm performs on this polygon to determine whether the first (green) point is in the polygon are, starting from the first edge:

1. Green Point crosses edge 8
2. Green Point does not cross edge 1
3. Green Point crosses edge 2
4. Green Point does not cross edge 3
5. Green Point crosses edge 4
6. Green Point crosses edge 5
7. Green Point does not cross edge 6
8. Green Point does not cross edge 7
9. Total number of crossings: 4
10. Even number of edge crossings, therefore the point is not in the polygon

The steps the algorithm performs on this polygon to determine whether the second (red) point is in the polygon are, starting from the first edge:

1. Red Point does not cross edge 8
2. Red Point does not cross edge 1
3. Red Point does not cross edge 2
4. Red Point does not cross edge 3
5. Red Point does not cross edge 4
6. Red Point crosses edge 5
7. Red Point does not cross edge 6
8. Red Point does not cross edge 7
9. Total number of crossings: 1
10. Uneven number of edge crossings, therefore the point is in the polygon

Runtime Complexity of the Algorithm

The runtime complexity of the Jordan Algorithm aka. Crossing Number Algorithm aka. Even-Odd Algorithm to solve the point-in-polygon problem for a single point is linear with respect to the number of edges. This is evident by looking at the code, which contains a single loop over the edges, with no recursion or further function calls or loops.

Formally the runtime is O(|V|), |V|:=number of edges in the polygon.

Space Complexity of the Algorithm

The space complexity is also linear w.r.t. the number of edges, since only fixed-size variables need to be stored in addition to the polygon. Additionally, the algorithm can be implemented on-line, meaning there is no need to look at past edges during the loop, so they can be evicted from memory (or comparable performance improvement measures).