The Breadth-first search algorithm is an algorithm used to solve the shortest path problem in a graph without edge weights (i.e. a graph where all nodes are the same “distance” from each other, and they are either connected or not). This means that given a number of nodes and the edges between them, the Breadth-first search algorithm is finds the shortest path from the specified start node to all other nodes. Nodes are sometimes referred to as vertices (plural of vertex) - here, we’ll call them nodes.

Description of the Algorithm

The basic principle behind the Breadth-first search algorithm is to take the current node (the start node in the beginning) and then add all of its neighbors that we haven’t visited yet to a queue. Continue this with the next node in the queue (in a queue that is the “oldest” node). Before we add a node to the queue, we set its distance to the distance of the current node plus 1 (since all edges are weighted equally), with the distance to the start node being 0. This is repeated until there are no more nodes in the queue (all nodes are visited).

In more detail, this leads to the following Steps:

1. Initialize the distance to the starting node as 0. The distances to all other node do not need to be initialized since every node is visited exactly once.
2. Set all nodes to “unvisited”
3. Add the first node to the queue and label it visited.

4. While there are nodes in the queue:

   1. Take a node out of the queue
   2. For all nodes next to it that we haven’t visited yet, add them to the queue, set their distance to the distance to the current node plus 1, and set them as “visited”

In the end, the distances to all nodes will be correct.

Example of the Algorithm

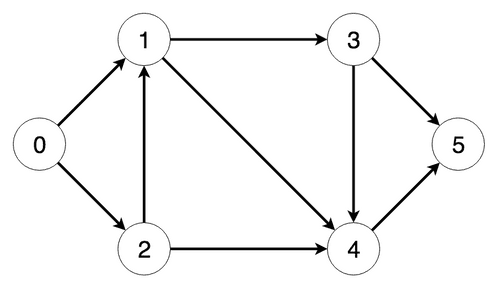
Consider the following graph:

The steps the algorithm performs on this graph if given node 0 as a starting point, in order, are:

1. Visiting node 0

2. Visited nodes: [true, false, false, false, false, false], Distances: [0, 0, 0, 0, 0, 0]

   1. Removing node 0 from the queue…
   2. Visiting node 1, setting its distance to 1 and adding it to the queue
   3. Visiting node 2, setting its distance to 1 and adding it to the queue

3. Visited nodes: [true, true, true, false, false, false], Distances: [0, 1, 1, 0, 0, 0]

   1. Removing node 1 from the queue…
   2. Visiting node 3, setting its distance to 2 and adding it to the queue
   3. Visiting node 4, setting its distance to 2 and adding it to the queue

4. Visited nodes: [true, true, true, true, true, false], Distances: [0, 1, 1, 2, 2, 0]

   1. Removing node 2 from the queue…
   2. No adjacent, unvisited nodes

5. Visited nodes: [true, true, true, true, true, false], Distances: [0, 1, 1, 2, 2, 0]

   1. Removing node 3 from the queue…
   2. Visiting node 5, setting its distance to 3 and adding it to the queue

6. Visited nodes: [true, true, true, true, true, true], Distances: [0, 1, 1, 2, 2, 3]

   1. Removing node 4 from the queue…
   2. No adjacent, unvisited nodes

7. Visited nodes: [true, true, true, true, true, true], Distances: [0, 1, 1, 2, 2, 3]

   1. Removing node 5 from the queue…
8. No more nodes in the queue. Final distances: [0, 1, 1, 2, 2, 3]

Runtime Complexity of the Algorithm

The runtime complexity of Breadth-first search is O(|E| + |V|) (|V| = number of Nodes, |E| = number of Edges) if adjacency-lists are used. If a we simply search all nodes to find connected nodes in each step, and use a matrix to look up whether two nodes are adjacent, the runtime complexity increases to O(|V|^2).

Depending on the graph this might not matter, since the number of edges can be as big as |V|^2 if all nodes are connected with each other.

Space Complexity of the Algorithm

The space complexity of Breadth-first search depends on how it is implemented as well and is equal to the runtime complexity.

Python

Python™ is an interpreted language used for many purposes ranging from embedded programming to web development, with one of the largest use cases being data science.

Getting to “Hello World” in Python

The most important things first - here’s how you can run your first line of code in Python.

1. Download and install the latest version of Python from python.org. You can also download an earlier version if your use case requires it - many technologies still require it due to the breaking changes introduced with Python 3.
2. Open a terminal, make sure the python or python3 command is working, and that the command your’re going to be using is referring to the version you just installed by running python3 --version or python --version. If you’re getting a “command not found” error (or similar), try restarting your command line, and, if that doesn’t help, your computer. If the issue persists, here are some helpful StackOverflow questions for Windows, Mac and Linux.
3. As soon as that’s working, you can run the following snippet: print("Hello World"). You have two options to run this: 3.1 Run python in the command line, just paste the code snippet and press enter (Press CTRL + D or write exit() and press enter to exit). 3.2 Save the snippet to a file, name it something ending with .py, e.g. hello_world.py, and run python path/to/hello_world.py. Tip: use the ls command (dir in Windows) to figure out which files are in the folder your command line is currently in.

That’s it! Notice how printing something to the console is just a single line in Python - this low entry barrier and lack of required boilerplate code is a big part of the appeal of Python.

Fundamentals in Python

To understand algorithms and technologies implemented in Python, one first needs to understand what basic programming concepts look like in this particular language.

Variables and Arithmetic

Variables in Python are really simple, no need to declare a datatype or even declare that you’re defining a variable; Python knows this implicitly.

a = 1
b = {'c':2}

print(a + b['c']) # prints 3

Arrays

Working with arrays is similarly simple in Python:

arr = ["Hello", "World"]

print(arr[0]) # Hello
print(arr[1]) # World
# print(arr[2]) # IndexError

arr.append("!")

print(arr[2]) # !

As those of you familiar with other programming language like Java might have already noticed, those are not native arrays, but rather lists dressed like arrays. This is evident by the fact that no size needs to be specified, and elements can be appended at will. In fact, print(type(arr)) prints <class 'list'>. This means that arrays in Python are considerably slower than in lower level programming languages. There are, however, packages like numpy which implement real arrays that are considerably faster.

Conditions

Just like most programming languages, Python can do if-else statements:

value = 1
if value==1:
    print("Value is 1")
elif value==2:
    print("Value is 2")
else:
    print("Value is something else")

Python does however not have case-statements that other languages like Java have. In my opinion, this can be excused by the simplicity of the if-statements which make the “syntactic sugar” of case-statements obsolete.

Loops

Python supports both for and while loops as well as break and continue statements. While it does not have do-while loops, it does have a number of built-in functions that make make looping very convenient, like ‘enumerate’ or range. Here are some examples:

value = 10
while value > 0:
    print(value)
    value -= 1

for index, character in enumerate("banana"):
    print("The %d-th letter is a %s" % (index + 1, character))

Note that Python does not share the common iterator-variable syntax of other languages (e.g. for(int i = 0; i < arr.length; i++) in Java) - for this, the enumerate function can be used.

Functions

Functions in Python are easily defined and, for better or worse, do not require specifying return or arguments types. Optionally, a default for arguments can be specified:

def print_something(something="Hello World"):
    print(something)
    return "Success"

print_something()
print(print_something("banana"))

(This will print “Hello World”, “Banana”, and then “Success”)

Syntax

As you might have noticed, Python does not use curly brackets ({}) to surround code blocks in conditions, loops, functions etc.; This is because Python depends on indentation (whitespace) as part of its syntax. Whereas you can add and delete any amount of whitespace (spaces, tabs, newlines) in Java without changing the program, this will break the Syntax in Python. This also means that semicolons are not required, which is a common syntax error in other languages.

Advanced Knowledge of Python

Python was first released in 1990 and is multi-paradigm, meaning while it is primarily imperative and functional, it also has object-oriented and reflective elements. It’s dynamically typed, but has started offering syntax for gradual typing since version 3.5. For more information, Python has a great Wikipedia article.