The A star (A*) algorithm is an algorithm used to solve the shortest path problem in a graph. This means that given a number of nodes and the edges between them as well as the “length” of the edges (referred to as “weight”) and a heuristic (more on that later), the A* algorithm finds the shortest path from the specified start node to all other nodes. Nodes are sometimes referred to as vertices (plural of vertex) - here, we’ll call them nodes.

Description of the Algorithm

The basic principle behind the A star (A*) algorithm is to iteratively look at the node with the currently smallest priority (which is the shortest distance from the start plus the heuristic to the goal) and update all not yet visited neighbors if the path to it via the current node is shorter. This is very similar to the Dijkstra algorithm, with the difference being that the lowest priority node is visited next, rather than the shortest distance node. In essence, Dijkstra uses the distance as the priority, whereas A* uses the distance plus the heuristic.

Why does adding the heuristic make sense? Without it, the algorithm has no idea if its going in the right direction. When manually searching for the shortest path in this example, you probably prioritised paths going to the right over paths going up or down. This is because the goal node is to the right of the start node, so going right is at least generally the correct direction. The heuristic gives the algorithm this spatial information.

So if a node has the currently shortest distance but is generally going in the wrong direction, whereas Dijkstra would have visited that node next, A Star will not. For this to work, the heuristic needs to be admissible, meaning it has to never overestimate the actual cost (i.e. distance) - which is the case for straight line distance in street networks, for example. Intuitively, that way the algorithm never overlooks a shorter path because the priority will always be lower than the real distance (if the current shortest path is A, then if there is any way path B could be shorter it will be explored). One simple heuristic that fulfils this property is straight line distance (e.g. in a street network)

In more detail, this leads to the following Steps:

1. Initialize the distance to the starting node as 0 and the distances to all other nodes as infinite
2. Initialize the priority to the starting node as the straight-line distance to the goal and the priorities of all other nodes as infinite
3. Set all nodes to “unvisited”

4. While we haven’t visited all nodes and haven’t found the goal node:

   1. Find the node with currently lowest priority (for the first pass, this will be the source node itself)
   2. If it’s the goal node, return its distance
   3. For all nodes next to it that we haven’t visited yet, check if the currently smallest distance to that neighbor is bigger than if we were to go via the current node
   4. If it is, update the smallest distance of that neighbor to be the distance from the source to the current node plus the distance from the current node to that neighbor, and update its priority to be the distance plus its straight-line distance to the goal node

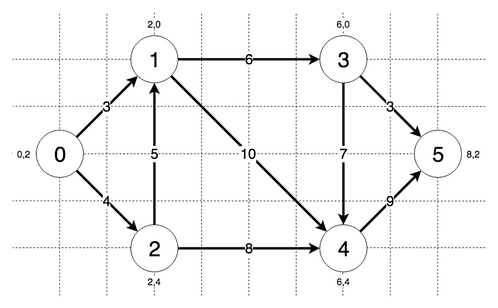
Example of the Algorithm

Consider the following graph:

The steps the algorithm performs on this graph if given node 0 as a starting point and node 5 as the goal, in order, are:

1. Visiting node 0 with currently lowest priority of 8.0
2. Updating distance of node 1 to 3 and priority to 9.32455532033676
3. Updating distance of node 2 to 4 and priority to 10.32455532033676
4. Visiting node 1 with currently lowest priority of 9.32455532033676
5. Updating distance of node 3 to 9 and priority to 11.82842712474619
6. Updating distance of node 4 to 13 and priority to 15.82842712474619
7. Visiting node 2 with currently lowest priority of 10.32455532033676
8. Visiting node 3 with currently lowest priority of 11.82842712474619
9. Updating distance of node 5 to 12 and priority to 12.0
10. Goal node found!

Final lowest distance from node 0 to node 5: 12

Runtime of the Algorithm

The runtime complexity of A Star depends on how it is implemented. If a min-heap is used to determine the next node to visit, and adjacency is implemented using adjacency lists, the runtime is O(|E| + |V|log|V|) (|V| = number of Nodes, |E| = number of Edges). If a we simply search all distances to find the node with the lowest distance in each step, and use a matrix to look up whether two nodes are adjacent, the runtime complexity increases to O(|V|^2).

Note that this is the same as Dijkstra - in practice, though, if we choose a good heuristic, many of the paths can be eliminated before they are explored making for a significant time improvement.

More information on how the heuristic influences the complexity can be found on the Wikipedia Article.

Space of the Algorithm

The space complexity of A Star depends on how it is implemented as well and is equal to the runtime complexity, plus whatever space the heuristic requires.