The Iterative Deepening A Star (IDA*) algorithm is an algorithm used to solve the shortest path problem in a tree, but can be modified to handle graphs (i.e. cycles). It builds on Iterative Deepening Depth-First Search (ID-DFS) by adding an heuristic to explore only relevant nodes.

Description of the Algorithm

Whereas Iterative Deepening DFS uses simple depth to decide when to abort the current iteration and continue with a higher depth, Iterative Deepening A Star uses a heuristic to determine which nodes to explore and at which depth to stop. This is similar to how Dijkstra always explores the node with the currently shortest difference and A Star adds an heuristic to this to only explore nodes that are actually closer to the goal.

In more detail, this leads to the following Steps:

1. For each child of the current node
2. If it is the target node, return
3. If the distance plus the heuristic exceeds the current threshold, return this exceeding threshold
4. Set the current node to this node and go back to 1.
5. After having gone through all children, go to the next child of the parent (the next sibling)
6. After having gone through all children of the start node, increase the threshold to the smallest of the exceeding thresholds.
7. If we have reached all leaf (bottom) nodes, the goal node doesn’t exist.

Example of the Algorithm

Consider the following graph:

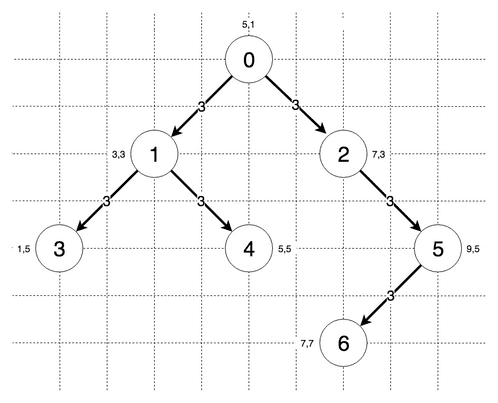
The steps the algorithm performs on this graph if given node 0 as a starting point and node 6 as the goal, in order, are:

1. Iteration with threshold: 6.32
2. Visiting Node 0
3. Visiting Node 1
4. Breached threshold with heuristic: 8.66
5. Visiting Node 2
6. Breached threshold with heuristic: 7.00
7. Iteration with threshold: 7.00
8. Visiting Node 0
9. Visiting Node 1
10. Breached threshold with heuristic: 8.66
11. Visiting Node 2
12. Visiting Node 5
13. Breached threshold with heuristic: 8.83
14. Iteration with threshold: 8.66
15. Visiting Node 0
16. Visiting Node 1
17. Visiting Node 3
18. Breached threshold with heuristic: 12.32
19. Visiting Node 4
20. Breached threshold with heuristic: 8.83
21. Visiting Node 2
22. Visiting Node 5
23. Breached threshold with heuristic: 8.83
24. Iteration with threshold: 8.83
25. Visiting Node 0
26. Visiting Node 1
27. Visiting Node 3
28. Breached threshold with heuristic: 12.32
29. Visiting Node 4
30. Visiting Node 2
31. Visiting Node 5
32. Visiting Node 6
33. Found the node we’re looking for!

Final lowest distance from node 0 to node 6: 9

Notice how the algorithm did not continue to explore down from node 3 in the iteration it found the goal node in. If node 3 would’ve had children, whereas Iterative Deepening DFS would’ve potentially (and needlessly!) explored them, Iterative Deepening A Star did not.

Runtime of the Algorithm

The runtime complexity of Iterative Deepening A Star is in principle the same as Iterative Deepening DFS. In practice, though, if we choose a good heuristic, many of the paths can be eliminated before they are explored making for a significant time improvement. More information on how the heuristic influences the complexity can be found on the Wikipedia Article.

Space of the Algorithm

The space complexity of Iterative Deepening A Star is the amount of storage needed for the tree or graph. O(|N|), |N| = number of Nodes in the tree or graph, which can be replaced with b^d for trees, where b is the branching factor and d is the depth. Additionally, whatever space the heuristic requires.

C is a compiled language used for many purposes, although it can be primarily found in systems where importance is important. This is because C offers a lot of low-level support for optimization, at the cost of not having some of the convenient abstractions that other languages offer. C is therefore primarily found in situations where available computation power is low such as embedded systems, or situations where required computation power is high, such as simulation or deep learning.

Getting to “Hello World” in C

The most important things first - here’s how you can run your first line of code in C.

1. If you’re on Linux or Mac, download and install the latest version of GCC, a C compiler, from gcc.gnu.org. You can also download an earlier version if your use case requires it.
2. If you’re on Windows, you can also install GCC, even though it might cause problems. You also have other options outlined e.g. here.

3. Open a terminal, make sure the gcc command is working (or the according command for whichever compiler you’re using), and that the command your’re going to be using is referring to the version you just installed by running gcc --version. If you’re getting a “command not found” error (or similar), try restarting your command line, and, if that doesn’t help, your computer. If the issue persists, here are some helpful forum questions for each platform:

   • Windows
   • Mac
   • Linux

4. As soon as that’s working, copy the following snippet into a file named HelloWorld.c:

   #include<stdio.h>
   int main() {
   printf("Hello World\n");
   return 0;
   }

5. Change directory by typing cd path/to/HelloWorld, then run gcc HelloWorld.c to compile the file (which creates the bytecode), then run ./a.out. This should print “Hello World” to your Terminal.

That’s it! People who know multiple programming languages will notice that the entry barrier in C is a little lower than Java even though it is lower-level, while the entry barrier to Python is lower even though it is higher-level. My personal observation is that low-level and high-level languages tend to have low barriers of entry, whereas mid-level languages have higher barriers.

Fundamentals in C

To understand algorithms and technologies implemented in C, one first needs to understand what basic programming concepts look like in this particular language. Each of the following snippets should be compiled and run using the commands mentioned above.

Variables and Arithmetic

Variables in C are statically typed, meaning the content of a variable needs to be specified when writing the code. The datatype for whole numbers, for example is int. Numbers with decimal places are typed float or double depending on the required precision. The type for text ist String.

#include<stdio.h>

int main() {
    int number = 5;
    double decimalNumber = 3.25;
    double result = number * decimalNumber;
    char callout [] = "The number is ";
    // In this instance, the values are concatenated rather than added because one of them is a String.
    printf("%s", callout);
    printf("%f", result);
    printf("\n");
    return 0;
}

Arrays

Arrays in C are real arrays (as opposed to e.g. Python where they’re implemented as lists). The implications of that are that the size needs to be set when they are created and cannot be changed, but also that they are more efficient in C than they are in Python. Also, contrary to Java, C does not check array bounds. If you access an index that doesn’t exist, the program will read whatever is in the memory at that location (which will probably be gibberish).

int integers[5];
integers[3] = 12; // Assigning values to positions in the array
printf("%d\n", integers[0]); // will be 0
printf("%d\n", integers[3]); // will be 12
printf("%d\n", integers[6]); // will print something random that happened to be at that location in memory
return 0;

Conditions

Just like most programming languages, C can do if-else statements. Additionally, C can also do switch-case statements.

int value = 5;
    if(value == 5){
        printf("%s\n", "Value is 5");
    } else if(value < 5){
        printf("%s\n", "Value is less than 5");
    } else {
        printf("%s\n", "Value is something else");
    }
    
    switch (value){
        case 1:
            printf("%s\n", "Value is 1");
            break; // Don't go further down the cases
        case 2:
            printf("%s\n", "Value is 2");
            break; // Don't go further down the cases
        case 3:
            printf("%s\n", "Value is 3");
            break; // Don't go further down the cases
        case 4:
            printf("%s\n", "Value is 4");
            break; // Don't go further down the cases
        case 5:
            printf("%s\n", "Value is 5");
            break; // Don't go further down the cases
        default:
            printf("%s\n", "Value is something else");
    }

The above C code will print “Value is 5” twice.

Loops

C supports for, while as well as do while loops. break and continue statements are also supported. The below example illustrates the differences:

int value = 2;
for (int i = 0; i < value; i++) {
    printf("%d\n", i);
}
while (value > 0) {
    printf("%d\n", value);
    value--;
}
do {
    printf("%d\n", value);
    value--;
} while (value > 0);

This will print the following to the terminal:

0
1
2
1
0

Note the last 0: it is printed because in the do-while-loop, compared to the while-loop. the code block is executed at least once before the condition is checked.

Functions

Functions in C can be declared similar to Java, but require less boilerplate since they don’t need to be part of classes or objects. Here is a minimal example of a function:

#include<stdio.h>

int addNumbers(int numberOne, int numberTwo) {
    return numberOne + numberTwo;
}

int main() {
    printf("%d\n", addNumbers(3, 4));
}

Syntax

C requires the use of curly brackets ({}) to surround code blocks in conditions, loops, functions etc.; It also requires semicolons at then end of statements. While this can lead to some annoying syntax errors, it also means the use of whitespace for preferred formatting (e.g. indentation of code pieces) does not affect the code. Note how the Syntax of C is very similar to Java. The Syntax of Java, and many other languages that came after and/or were derived from C copy many aspects of its Syntax.

Advanced Knowledge of C

C was first released in 1972, is statically typed and was ported to many platforms with various implementations (one of which is GCC which was presented in this article). For more information, C has a great Wikipedia) article.